ACMSimC: Modeling Saturation
今天开始,我会慢慢停止过家家,然后逐渐开始介绍一些逼近我的知识边界的内容。所以,内容可能有不准确之处,请自行辨别。
Introduction
截至目前,我们用的感应电机模型或永磁电机模型,都是作了超多的假设的,我这里提三点。
第一点,基波模型假设。很多人都知道这个词,但是又可能说不出个所以然来,要我来说,就是在用绕组函数推导电感表达式的时候,作了绕组函数关于气隙空间位置是正弦波的假设,本质上等价于假设绕组的匝数是正弦分布于气隙中的——此处的“绕组在气隙中”暗示忽略了齿槽效应。对于常见的齿数比较多的中大型感应电机来说,由于分布、短距(暗示双层绕组)、斜槽(削弱齿槽效应的两个源头中的一个)的加持,这么假设感觉还是很合理的。
这里抛一个问题:对于每极每相槽数不为整数的分数槽电机来说,咱们还用基波模型吗?对于利用所谓的“磁场调制效应”产生“额外”转矩的电机(比如开关磁链电机和游标电机)来说,咱们还用基波模型吗?
关于答案就不要问我了,我也不清楚,哈哈。
第二点,忽略铁耗电阻。我们打开标准 IEEE Std 112-2017,找到感应电机的等效电路图如下:
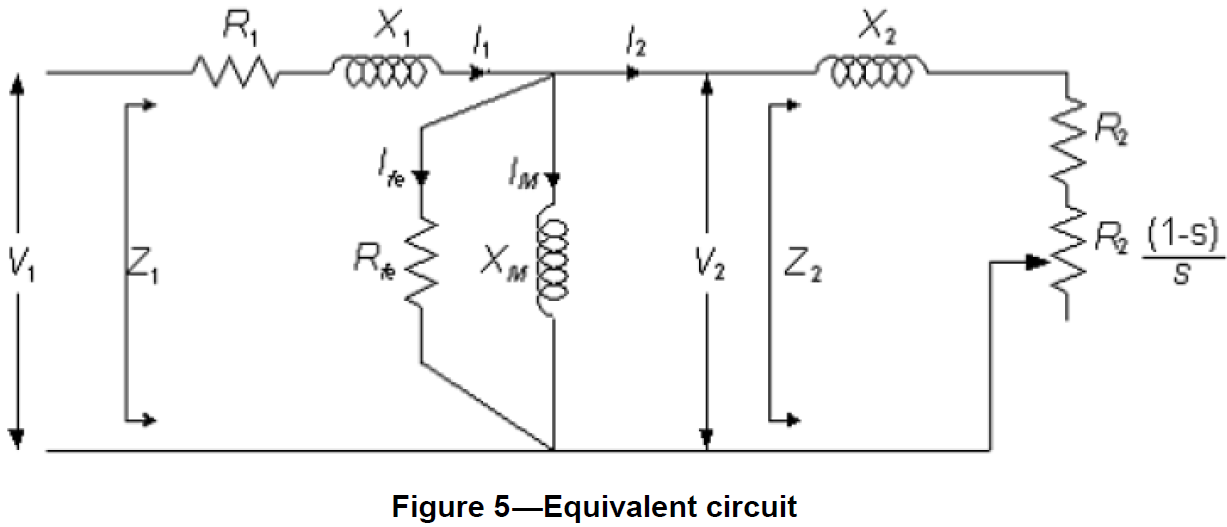
这里的 $R_{fe}$ 就是铁耗电阻,一般阻值在 1000 Ohm 这个量级。根据空载试验和堵转实验,可以拿到在某些个频率点下的铁耗电阻值,再根据那个 Steinmetz’s equation 拟合一下,就可以查表使用了。
第三点,忽略饱和现象。相比前面两点,这一点的影响其实是最大的。比如,仿真里,只要你 M 轴电流使劲给,磁链弄出个 20 Wb (额定比如说是 1.0 Wb)都没有问题——这在现实中是不可能的。
所以,今天,咱们就是要把磁路中的铁芯随着磁场强度的增强,其磁导率最终(不一定是单调的)减小的现象给建个模。在电路中,该现象表现为励磁电感随着励磁电流的变化而变化。
IM Model Using Fluxes as States
定、转子磁链解算(这一步是唯一的数值积分步)
我就不绕弯了,文献是 Therrien et al. 2013,状态变量得选为定、转子磁链。
\[\left\{ \begin{array}{l} p{\psi _{qs}} = {u_{qs}} - {r_s}{i_{qs}} - \omega {\psi _{ds}}\\ p{\psi _{ds}} = {u_{ds}} - {r_s}{i_{ds}} + \omega {\psi _{qs}}\\ p{\psi _{qr}} = - {r_r}{i_{qr}} - \left( {\omega - {\omega _r}} \right){\psi _{dr}}\\ p{\psi _{dr}} = - {r_r}{i_{dr}} + \left( {\omega - {\omega _r}} \right){\psi _{qr}} \end{array} \right.\]对上面这个动态方程(当然还要加上转子运动方程)进行仿真,你应该感到没有任何压力,因为电感压根没出现,但是电流从哪里来?
强调一下,这边的 d-q 系是定子静止坐标系。本身在感应电机建模中讲 d-q 坐标系就很反常了,所以不应该出现误解。为什么原作者要这么做?因为他们要提出一个感应电机和同步电机通用的模型。
z标电流解算(查表用电流)
根据当前步的磁链状态,得到以z为下标的电流。
\[\left\{ \begin{array}{l} {i_{zq}} \buildrel \Delta \over = \left( {\frac{{{\psi _{qs}}}}{{{L_{ls}}}} + \frac{{{\psi _{qr}}}}{{{L_{lr}}}}} \right) = {i_{mq}} + \left( {\frac{1}{{{L_{ls}}}} + \frac{1}{{{L_{lr}}}}} \right){\psi _{mq}}\\ {i_{zd}} \buildrel \Delta \over = \left( {\frac{{{\psi _{ds}}}}{{{L_{ls}}}} + \frac{{{\psi _{dr}}}}{{{L_{lr}}}}} \right) = {i_{md}} + \left( {\frac{1}{{{L_{ls}}}} + \frac{1}{{{L_{lr}}}}} \right){\psi _{md}} \end{array} \right.\]据此可知,这个模型的唯一缺点,就是不能假设转子漏感 Llr 为零——然而,在简单模型中该假设是合法的。
如果z电流向量的幅值大于零,那么就拿来查表:$\psi_m=G(i_z)$。如何获得该表?请根据下式来弄:
\[i_z=\sqrt{i_{zq}^2+i_{zd}^2}=i_m+\psi_m/L_{\Sigma l}\]式中,$L_{\Sigma l}=(1/L_{ls}+1/L_{lr})^{-1}$ ,物理意义感觉是把定、转子漏感并联起来所得的漏电感?所谓的饱和曲线,就是指励磁电流$i_m$和气隙磁链$\psi_m$的关系。
气隙磁链结算
气隙磁链可以用你的表和z标电流进行求解:
\[\left\{ \begin{array}{l} {\psi _{mq}} = {\psi _m}\frac{{{i_{zq}}}}{{{i_z}}} = G\left( {{i_z}} \right)\frac{{{i_{zq}}}}{{{i_z}}}\\ {\psi _{md}} = {\psi _m}\frac{{{i_{zd}}}}{{{i_z}}} = G\left( {{i_z}} \right)\frac{{{i_{zd}}}}{{{i_z}}} \end{array} \right.\]电流解算
求电流就是先求漏磁链,除以漏电感就是了。
\[\left\{ \begin{array}{l} {i_{qs}} = \frac{{{\psi _{qs}} - {\psi _{mq}}}}{{{L_{ls}}}}\\ {\psi _{ds}} = {L_{ls}}{i_{ds}} + {\psi _{md}}\\ {i_{qr}} = \frac{{{\psi _{qr}} - {\psi _{mq}}}}{{{L_{lr}}}}\\ {\psi _{dr}} = {L_{lr}}{i_{dr}} + {\psi _{md}} \end{array} \right.\]这里已经全了——定转子的d、q轴电流——不要被形式所迷惑。这边求得的电流,带入到定、转子磁链结算那一步,你的数值积分求解器就能跑下去了。
m标电流解算(此步没有任何实际意义,请跳过)
根据当前步的磁链状态导出以m为下标的电流。
\[\left\{ \begin{array}{l} {i_{mq}} = \left( {\frac{{{\psi _{qs}}}}{{{L_{ls}}}} + \frac{{{\psi _{qr}}}}{{{L_{lr}}}}} \right) - \left( {\frac{{{\psi _{mq}}}}{{{L_{ls}}}} + \frac{{{\psi _{mq}}}}{{{L_{lr}}}}} \right)\\ {i_{md}} = \left( {\frac{{{\psi _{ds}}}}{{{L_{ls}}}} + \frac{{{\psi _{dr}}}}{{{L_{lr}}}}} \right) - \left( {\frac{{{\psi _{md}}}}{{{L_{ls}}}} + \frac{{{\psi _{md}}}}{{{L_{lr}}}}} \right) \end{array} \right.\]代码实现
为了第一次看到本文的读者,我啰嗦一下,代码在我的 Github 页面上,对于代码的解释,我倾向于使用视频教程的形式进行介绍,这样更符合二十一世纪的风格。
哔哩哔哩传送门:https://www.bilibili.com/video/av63771498/
结语
为了让本文的考虑饱和的模型真正有效,
- 要么得用有限元把你设计好的感应电机的饱和曲线给辨识出来,
- 要么得做实验把你的样机的饱和曲线给辨识出来, 不出意外,这些内容会陆续介绍的。
本文针对感应电机写作,实际上该饱和模型同样适用于同步电机,具体请参考 Therrien 2013。
Therrien, F., Wang, L., Jatskevich, J., & Wasynczuk, O. (2013). Efficient explicit representation of AC machines main flux saturation in state-variable-based transient simulation packages. IEEE Transactions on Energy Conversion, 28(2), 380-393.
Future Topics (Updated)
- C语言电机仿真架构 / framework in C language (done in EP01)
- 矢量控制 / Vector control (done in EP02)
- 永磁电机的仿真 (done in EP03)
- 为什么前向欧拉法是个大坑?
- 永磁电机的滑模观测器
- 系统控制参数的可视化与优化框架 / Visualization and optimization of system control parameters
- 电机设计的电路参数拟合
- 变步长数值积分 / DoPri54
- 电机参数自整定
- 电流环系数设计
- 电压电流解耦电路 (done in EP04)
- 转速环系数设计
- 转动惯量辩识
- 无速度传感器系统中的转动惯量辨识
- 自抗扰控制
- 基于带宽指标的自抗扰控制系数设计
- 预测控制(预测电流控制,PCC)与优化目标
- 全局稳定转速自适应观测器设计
- 一种简单的自适应观测器(模型参考自适应系统,MRAS)设计及其存在的问题 (done in EP05)
- 逆变器非线性建模 / inverter nonlinearity
- SPWM建模
- SVPWM建模
- 饱和建模 / modeling of saturation (done in this article as EP06)
- 结合场的建模策略(查表法)
- 如何绘制任意控制策略的电机运行工况效率图?
- 非理想电流测量环节建模(温飘与不对称)
- 母线电容建模和无轴承电机的仿佛有UPS控制
- 异步伺服(异步电机的位置控制媲美永磁电机的关键是?)
- 低成本单母线电流传感器驱动的实现
- 无轴承感应电机建模
- 基于扩展反电势模型的无传感器控制
- 基于 Active Flux 模型的无传感器控制
- 三维模型的绘制技巧 / SolidWorks Modeling (done)
- 番外:使用免费有限元软件实现感应电机的设计与优化 (done 1/4)
- 番外:使用旋转静态场有限元实现电机转矩脉动的超准确分析(嗯,堪比瞬态场)
- 番外:Notched Rotor(介于表贴和内嵌之间的一种转子)永磁电机的设计
- 番外:高速实心转子的设计与优化
- 番外:机器学习之电机建模竞赛
Leave a comment